Chaque année, j’essaie de transmettre ce que je crois être la beauté des mathématiques lorsque j’enseigne l’optimisation convexe à l’EPFL. J’ai déjà mentionné sur ce blog quelques beaux livres de vulgarisation sur le sujet. Quelques lectures récentes m’ont convaincu encore plus et laissez moi essayer de vous convaincre également.
Alain Badiou est un choix assez surprenant pour parler de mathématiques, mais j’aime ce qu’il a récemment écrit: « Ce sentiment quasi esthétique des mathématiques m’a frappé très tôt. […] Je pense à la droite d’Euler. On montrait que les trois hauteurs d’un triangle sont concourantes en un point H, c’était déjà beau. Puis que les trois médiatrices l’étaient aussi, en un point O, de mieux en mieux ! Enfin que les trois médianes l’étaient également, en un point G ! Formidable. Mais alors, avec un air mystérieux, le professeur nous indiquait que l’on pouvait démontrer comme l’avait fait le génial mathématicien Euler, que ces points H, O, G étaient en plus tous les trois sur une même droite, qu’on appelle évidemment la droite d’Euler ! C’était si inattendu, si élégant, cet alignement de trois points fondamentaux, comme comportement des caractéristiques d’un triangle ! […] Il y a cette idée d’une découverte véritable, d’un résultat surprenant au prix d’un cheminement parfois un peu difficile à suivre, mais où l’on est récompensé. J’ai souvent comparé plus tard les mathématiques à la promenade en montagne : la marche d’approche est longue et pénible, avec beaucoup de tournant, de raidillons, on croit être arrivé, mais il reste encore un tournant… On sue, on peine, mais quand on arrive au col, la récompense est sans égale, vraiment : ce saisissement, cette beauté finale des mathématiques, cette beauté sûrement conquise, absolument singulière. » [Pages 11-12]
Une autre source d’inspiration est Proofs_from_THE_BOOK (Raisonnements divins). Ecrit en hommage à Paul Erdös, le livre commence par les deux pages ci-dessus. « Paul Erdös aimait parler du Livre, dans lequel Dieu maintient les preuves parfaites des théorèmes mathématiques, suivant le dicton de G. H. Hardy qu’il n’y a pas de place durable pour la laideur dans les mathématiques. Erdös avait également déclaré que vous n’avez pas besoin de croire en Dieu mais, en tant que mathématicien, vous devriez croire au Livre. […] Nous n’avons aucune définition ou caractérisation de ce qui constitue une preuve du Livre: tout ce que nous offrons ici sont les exemples que nous avons sélectionnés, en espérant que nos lecteurs partageront notre enthousiasme pour des idées brillantes, des idées intelligentes et de merveilleuses observations ».
Il m’arrive d’essayer de me souvenir des démonstrations les plus belles que j’ai « ressenties » depuis mes années de lycéen.
– La plus lumineuse, la démonstration par Gauss de la somme des n premiers entiers.
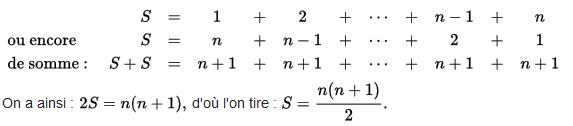
– Deux démonstrations du théorème de Pythagore.
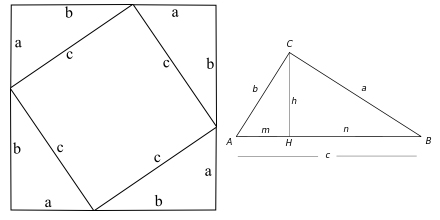
– Il y en aurait beaucoup d’autres comme l’infinité des nombres premiers, le développpement en série de ∏ (
), la très belle conception de la dualité pour les ensembles convexes (vous pouvez regarder un ensemble à travers ses points « interieurs » ou à travers l’enveloppe duale « extérieure » faite de ses tangentes).
– Mais la plus fascinante pour moi, reste l’utilisation de la Diagonale de Cantor:
[De Wikipedia:]
Pour démontrer que ℝ est non dénombrable, il suffit de démontrer la non-dénombrabilité du sous-ensemble [0,1[ de ℝ, donc de construire, pour toute partie dénombrable D de [0,1[, un élément de [0,1[ n’appartenant pas à D.
Soit donc une partie dénombrable de [0, 1[ énumérée à l’aide d’une suite r = (r1, r2, r3, … ). Chaque terme de cette suite a une écriture décimale avec une infinité de chiffres après la virgule (éventuellement une infinité de zéros pour un nombre décimal), soit :
- ri = 0, ri1 ri2 … rin …
On construit maintenant un nombre réel x dans [0,1[ en considérant le n-ième chiffre après la virgule de rn. Par exemple, pour la suite r :
- r1 = 0, 0 1 0 5 1 1 0 …
- r2 = 0, 4 1 3 2 0 4 3 …
- r3 = 0, 8 2 4 5 0 2 6 …
- r4 = 0, 2 3 3 0 1 2 6 …
- r5 = 0, 4 1 0 7 2 4 6 …
- r6 = 0, 9 9 3 7 8 1 8 …
- r7 = 0, 0 1 0 5 1 3 0 …
- …
Le nombre réel x est construit par la donnée de ses décimales suivant la règle : si la n-ième décimale de rn est différente de 1, alors la n-ième décimale de x est 1, sinon la n-ième est 2. Par exemple avec la suite ci-dessus, la règle donne x = 0, 1 2 1 1 1 2 1 …
Le nombre x est clairement dans l’intervalle [0, 1[ mais ne peut pas être dans la suite ( r1, r2, r3, … ), car il n’est égal à aucun des nombres de la suite : il ne peut pas être égal à r1 car la première décimale de x est différente de celle de r1, de même pour r2 en considérant la deuxième décimale, etc.
La non-unicité de l’écriture décimale pour les décimaux non nuls (deux écritures sont possibles pour ces nombres, l’une avec toutes les décimales valant 0 sauf un nombre fini, l’autre avec toutes les décimales valant 9 sauf un nombre fini) n’est pas un écueil au raisonnement précédent car le nombre x n’est pas décimal, puisque son écriture décimale est infinie et ne comporte que les chiffres 1 et 2.
Je vais terminer par une dernier extrait de Badiou (page 82): « J’appelle vérités (toujours au pluriel, il n’y a pas la « vérité ») des créations singulières à valeur universelle : œuvres d’art, théories scientifiques, politiques d’émancipation, passions amoureuses. Disons pour couper au plus court : les théories scientifiques sont des vérités concernant l’être lui-même (les mathématiques) ou les lois « naturelles » des mondes dont nous pouvons avoir une connaissance expérimentale (physique et biologie). Les vérités politiques concernent l’agencement des sociétés, les lois de la vie collective et de sa réorganisation, tout cela à la lumière de principes universels, comme la liberté, et aujourd’hui, principalement, l’égalité. Les vérités artistiques se rapportent à la consistance formelle d’œuvres finies qui subliment ce que nos sens peuvent recevoir : musique pour l’ouïe, peinture et sculpture pour la vision, poésie pour la parole… Enfin, les vérités amoureuses portent sur la puissance dialectique contenue dans le fait d’expérimenter le monde non à partir de l’Un, de la singularité individuelle, mais à partir du Deux, et donc dans une acceptation radicale de l’autre. Ces vérités ne sont pas, on le voit, de provenance ou de nature philosophique. Mais mon but est de sauver la catégorie (philosophique) de vérité qui les distingue et les nomme, en légitimant qu’une vérité puisse être :
-absolue, tout en étant une construction localisée,
-éternelle, tout en résultant d’un processus qui commence dans un monde déterminé et appartient donc au temps de ce monde. »