“Mathematicians are the humans who advance human understanding of mathematics.” William P. Thurston

I had already mentioned David Bessis’ book, Mathematica, when the author appeared on France Culture. He had spoken of Grothendieck, but said above all that between logic and intuition, he gave more importance to the second to do mathematics. Go back to the article to find the interview link. I had the chance to read his very beautiful book in the recent days and the author is convincing. He explains quite well the failure of the teaching of mathematics which gives too much importance to the first.

No doubt it will be difficult to change the minds of skeptics, but the argument that there is no special talent or gift for doing mathematics but above all curiosity and perseverance, as for any activity that requires learning, is well illustrated in his book.

It is not a question of tricks that are used too often in the teaching of mathematics, which can make people less fond of the discipline. In the article on the Beauty of Mathematics, I wrongly and a little too much used this impression of magic. It is more a question of deep understanding of things, in the sense that we end up seeing them. The downside of math is that while music is heard, or a sport is physically visible, math is mostly made up of mental images.

He also talks (as I must have done if you follow the #mathematics hashtag) about proofs of the sum of the first natural numbers and Bessis is luminous when he explains that Gauss’ clever proof probably does not really allow to “understand” the solution:

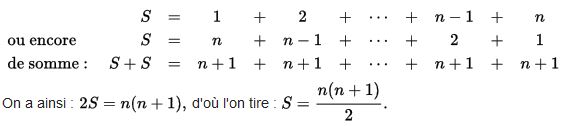
while there are more intuitive approaches such as the use of triangles or distance from the mean. Read his pages 169 to 181, it is easy to understand why Thurston as a child first gave 5000 as an answer to the sum of the first 100 integers, then corrected himself to give the exact answer. The average of a random drawing of numbers between 1 and 100 is also not quite 50… (unlike that between 0 and 100) and there is a link between the two subjects.

I really liked the descriptions and portraits that Bessis makes of Descartes, Thurston, Grothendieck and the less famous Ben Underwood. Or the magnificent passages on Pierre Deligne and Jean-Pierre Serre. I hope to give you the desire to discover them.

It is a beautiful book to offer to anyone who wishes to discover or rediscover the beauty of mathematics. And perhaps more importantly, as the subtitle of the book indicates, an adventure in the heart of ourselves, Bessis shows that all explorations are above all a choice to overcome one’s fears, to accept the possibility of mistakes, and the possibility of a path to more self-confidence. A paradox is an advice that comes up often in his book: “You should never read math books”. Except this one! Superb!