Author Archives: Hervé Lebret

The World of Startups according to Marion Flécher (Part 2)

In my post of November 8th, I promised to “read Marion Flécher’s book with great interest and will write to you in a future post to see if I find cause for resignation or optimism regarding the startup world.” I’m going to say both! The book is indeed excellent and perfectly describes the differences between France (which tried to claim to be a Startup Nation) and Silicon Valley (which never felt the need for such a claim).

The Difficulty of Defining the Word “Startup”

The heart of the book is not the comparison between the two regions, but rather what the French startup scene is like; I will return to this point. In her introduction, she explains the difficulty in defining the word, to the point of writing: “Making startups my subject of study was not a given. […] I was encouraged to use alternative terms such as innovative companies, technology companies, or high-growth companies” [page 16]. With a striking analogy, she adds, “as with the art world, in which players spend their time trying to determine what is art and what is not, it is by observing how a world makes these distinctions, and not by trying to make them ourselves, that we begin to understand what is happening in that world” [page 20]. Without naming Steve Blank, through a survey of entrepreneurs who gave her a multitude of definitions, she almost mentions my favorite definition: “a temporary organization in search of a repeatable and scalable business model”.

Silicon Valley, Heart of Startups

In her first chapter, Marion Flécher describes Silicon Valley, the region that gave rise to the semiconductor, the microprocessor, the microcomputer, software, the internet, social networks (and ultimately artificial intelligence, which had not yet emerged when she conducted her research). She demonstrates that the region was at the heart of a revolution that goes beyond technological innovation. This innovation was “accompanied by organizational and managerial innovations that led to a profound ideological redefinition of the entreprise” [page 52].

Yet, she shows that pinpointing the moment of their emergence is just as difficult as defining startups. “For many historians and ethnologists specializing in Silicon Valley, it is Intel’s invention of the microprocessor that constitutes the true starting point of the region’s technological boom and rise to power” [page 39]. She does not, however, neglect to note the importance of Hewlett-Packard (founded in 1939) and Fairchild (founded in 1957) in this dual revolution, including the development of project-based work in small teams, the upheaval of dress codes, and the implementation of new incentive structures [pages 52-53]. The complexity of the region’s origins also stems from the existence of other significant influences such as free software and the “Do It Yourself” culture [pages 55-56], and from a diversity of major players including venture capital funds, the federal government, and the companies themselves. A world, as the author describes it, an ecosystem.

Another difficulty addressed by Marion Flécher, at least for a Silicon Valley enthusiast like myself, is: when did the word “startup” first appear? “The term ‘startup’ seems to have been used for the first time in 1976, in a Forbes magazine article, to refer to young technology companies in Silicon Valley” [Author’s note: The Unfashionable Business of Investing in Startups in the Electronic Data Processing Field]. “The term ‘startup company’, which associates the startup with a specific type of business, appeared a year later in an article entitled ‘An Incubator for Startup Companies, Especially in the Fast-growth, High Technology Fields,’ published in Business Week in 1977.” The author adds that the term acquired its current meaning and spread worldwide during the 1990s, even though this new business model can be traced back to the 1940s. NB: I confirm this in a blog post: When was the word “start-up” first used?

Scan of Figure 2 [page 43]: Timeline of the main Silicon Valley technology companies. I circled two things by hand while reading. My surprise at seeing only one founder for eBay; I thought Jeff Skoll was a co-founder, but apparently he may have only been the first employee. And my other surprise at seeing three co-founders for Apple, which is rarely mentioned. Ronald Wayne is often forgotten. And then a rather unimportant note for Marion Flécher: Wo[lk]zniak is misspelled on page 41!

Risk and Uncertainty

In a brief but equally excellent section on venture capital, Marion Flécher explains that “unlike risk, which refers to a situation that can be predicted by probability and in which actors can reason rationally […] uncertainty refers to a situation in which the degree of singularity is such that it cannot be compared to any other. By developing disruptive innovations, Silicon Valley entrepreneurs create situations of radical uncertainty in which actors can only make speculative judgments” [page 46]. This explains why the term [ad]venture capital is very different from the term capital-risque in France (which is undoubtedly indicative of dissimilar worlds). “Nevertheless, these players have resources that allow them to transform the uncertainty of a situation into a quantifiable risk. Their activity requires, first and foremost, a sound knowledge of the technical environment, which enables them to assess the growth prospects of projects. Most investors […] are thus often former engineers or entrepreneurs” [page 47]. This is undoubtedly another major difference between Silicon Valley and France.

Since I mentioned personal surprises in the commentary on the figure above, I take this opportunity to add a few more personal comments (for myself, the author, and any potential reader!):
– Without a doubt, the startup world is a new illustration of capitalism, and this has undoubtedly been misunderstood. Startups have never been liberated companies; trade unions are very rare, not to say unwelcome. I already mentioned this point in my first post.
– Marion Flécher emphasizes intellectual property (Microsoft’s proprietary software, Intel’s microprocessor patent), which creates near-monopolies favored by a state that “seems to have implicitly supported market concentration” [page 49]. Yet it was the state that forced Bell Labs to grant licenses for the transistor, for which the company held the patent. Intel certainly had a near-monopoly on the microprocessor, even though IBM and AMD were genuine competitors. But competition in new sectors has made Intel a declining player in recent years (telecommunications, artificial intelligence). I would say that the US government is protecting the country at a macroeconomic level by defending its technological lead rather than protecting any individual company. OpenAI might replace Google, which could have replaced Microsoft, just as Nvidia or even AMD might replace Intel. The same goes for mobile phones. The US remains the leader.
– Another minor point of doubt: “Between 1998 and 1999, venture capital almost doubled, going from $3.2 billion to $6.1 billion” [page 48]. I have the impression, and I could be wrong, that the amounts were about ten times larger and that these figures correspond more closely to the 1980s.
– Finally, I see confirmation of a personal impression regarding the decrease in the number of IPOs: Silicon Valley had 417 IPOs in 2000 compared to only 14 in 2021 [page 51]. Indeed, for years I’ve been compiling market capitalization tables and dreamed of quickly reaching 1,000, but the IPO drought is slowing my ambition… On the other hand, M&A acquisitions still seem as prosperous as ever, since Marion Flécher mentions more than 90 acquisitions by Facebook since its creation (see my posts on Cisco and Google). A startup may not be destined to become a long-term business, but it’s also possible that the monopolistic concentration mentioned above is at its peak…

France, a nation of startups?

That’s the title of Chapter 2. And the second page of this chapter includes the following figure. It’s easy to see that the French press began to take an interest in the subject during the dot-com bubble and then again from 2012 onwards. Manon Flécher explains that this second period is significant, coinciding with the arrival of Uber and Airbnb in France, but also with the creation of BPIFrance and the French Tech initiative. Equally interesting, the author reminds us that General de Gaulle visited San Francisco in 1960, Georges Pompidou 10 years later, and François Mitterrand in 1984. The author doesn’t mention the creation of Sophia Antipolis in 1969, which Paul Graham mocks, more or less gently (see my post from 2011). Presidents Hollande and then Macron have been apparently much more involved in the topic.

Is France a startup nation? The answer is clear if you’ve read the preceding paragraphs. But the debate runs deeper, as I indicated in *Politics vs. Economics: A Country Is Not a Startup*, translating the article Non, la France ne doit pas devenir une start-up. I didn’t know, or had forgotten, that Emmanuel Macron had then used the term “hyper-innovation.” But the doomsayers are always ignored, and hyper-communication too often trumps reality and facts.

Marion Flécher also addresses this by stating that “despite this growth, the State remains the primary funder of startups in France” [page 71]. Her footnote on page 69 is revealing. “In 2015, business angels reportedly invested a total of €41 million, which was still half the amount in the United Kingdom and 2.5 times less than in Germany. […] In 2023, the United Kingdom continued to lead other European countries with €307.4 million invested by business angels, compared to €198.5 million for Germany and €142.5 million for France.” BPIFrance represents two billion euros in direct investments in company capital [page 72].

My post is already too long, which is convenient since I’m at this point in my reading of Le Monde des startups. Yet I haven’t even started on the main topic: the sociology of startup founders. A sequel coming soon!

Post-scriptum : On a related note, I just bought *Palo Alto: A History of California, Capitalism, and the World*, one review of which says, The most comprehensive — and incendiary — history of the place that we’re ever likely to get. A sweeping and unsparing critique, it’s also well written, frequently surprising and, because history tends to rhyme, increasingly urgent. You may never think about Stanford, iconic tech companies like Hewlett Packard or, indeed, the Valley itself the same way again. I won’t.” LOS ANGELES TIMES

The introduction already haunts me: the author promises to explain that the inhabitants of California, Silicon Valley and Palo Alto have not all forgotten the ghosts that surround them and without which the region could not have become what it is… To be continued!

The World of Startups by Marion Flécher

Leave a reply

The startup world has been the core of my professional life for almost 30 years. I know it perhaps too well, and I also read almost everything I can get my hands on. So I feel compelled to read a book that takes this subject as its title. Marion Flécher is a lecturer in sociology at the University of Paris Nanterre, and her book, *The World of Startups* (Le monde des startup) is based on her doctoral thesis, entitled *The Startup World: The New Face of Capitalism? An Investigation into the Modes of Creation and Organization of Startups in France and the United States*. (Le monde des start-up, le nouveau visage du capitalisme ? Enquête sur les modes de création et d’organisation des start-up en France et aux Etats-Unis).

Marion Flécher just post an article on LinkedIn pand she was alos the guest of Guillaume Erner yesterday morning on France Culture.

As you may have guessed, I haven’t read the book yet, but I will as soon as I receive it. I’m always a bit ambivalent when I read critical analyses of this world, and of Silicon Valley in particular. Here’s what the publisher says on the book’s page: “The book compares the promises made by startups (success stories, meritocracy, flexibility) with the reality on the ground (failure rates, mass layoffs, pressure to perform, burnout). For the past fifteen years or so, young, innovative companies grouped under the term “startups” have occupied an increasingly prominent place in the media and political arena. Symbols of modernity and Capitalism 2.0, they are being held up as a genuine economic and organizational model. How can we understand this enthusiasm? (…) Dismissing the mythical figure of the self-made man, she sheds light on the reality of this social world and defines the profile of those, and more rarely those women, who launch startups and claim this label. While they claim to break with the hierarchical rigidity of traditional firms, startups offer a new face of capitalism, one whose gentler and more colorful aspects have allowed it to recover from its critics. In the digital age and the era of new technologies, what do they foreshadow for the future of work?”

I am ambivalent for two reasons :

– The first reason is that it seems to me France has gone from a profound ignorance of this world to a critique of its excesses that is undoubtedly justified but harsh.

About ten years ago, Professor Libero Zuppiroli brilliantly criticized the unfulfilled promises of innovation in *The Utopias of the 21st Century*. A few years earlier, he had teased me about the fact that startups didn’t represent much at all. That was the subject of another post.

He was right, at least for Europe, to the point that neither France nor Europe has generated any real success stories. My previous post last week celebrated an EPFL’s success story at $3 billion, and Criteo, Mistral, and others are all modest in size compared to the behemoths that the GAFAMs have become. SAP, Spotify, ARM, and only a few others in Europe can be compared to American successes. I am therefore sometimes torn between comparing and criticizing two continents that have little in common. France has moved very quickly, not to say too quickly, from a lack of understanding to a criticism of this world without grasping the reasons for its appeal and success.

– The second reason is that this criticism has existed for a long time, and I’m saddened that communication takes precedence over information. Startups have never been a paradise; they are rarely liberated companies, so storytelling has transformed a few exceptions into a universal model.

For example in 1986 in Startup fever, one could read “The Silicon Valley has been called “one of the last great bastions of male dominance” by the local Peninsula Times Tribune. […] They are under-represented in management and administration. Few women have technical or engineering backgrounds. […] Why there are few women in positioning of responsability in Silicon Valley is complex and puzzling. Until recently, the overwhelming majority of engineering graduates were men. […] Scientific and engineering professionals in the finance community and in start-ups are likely to be men: these power-brokers rely exclusively on their personal networks. […] Twenty of the largest publicly held Silicon Valley firms listed a total of 209 persons as corporate officers in 1980; only 4 were women. The board of directors of these 20 firms include 150 directors. Only one was a woman: Shirley Hufstedler, serving on the board of Hewlett-Packard.” But the authors are optimistic: they explain that any woman with a technical background or an interest in high-tech has opportunities: “A Martian with three heads could find a job in Silicon Valley. So for women with a technical background, it’s terrific. […] An exception to masculine dominance is Sandy Kurtzig. “I wanted to start in a garage like HP, but I didn’t have one. So I started in a second bedroom of my apartment.” At first, Kurtzig did sales, bookkeeping and management of her start-up. As long as she had only five or six employees, they worked out of her apartment. It went into rapid growth and had annual sales in 1982.”

And what about Anna-Lee Saxenian in 1999 : “In 1979, I was a graduate student at Berkeley and I was one of the first scholars to study Silicon Valley. I culminated my master’s program by writing a thesis in which I confidently predicted that Silicon Valley would stop growing. I argued that housing and labor were too expensive and the roads were too congested, and while corporate headquarters and research might remain, I was convinced that the region had reached its physical limits and that innovation and job growth would occur elsewhere during the 1980s. As it turns out I was wrong.” Returning to the earlier statement (France has moved very quickly, not to say too quickly, from a lack of understanding to a criticism of this world without grasping the reasons for its appeal and success), I believe it is essential to read and reread the remarkable works of Professor Saxenian (Regional Advantage, The New Argonauts). She has been able to explain the reasons for these attractions and successes, which persist today despite the excesses.

I’ve arrived at these compromises, which the great Bernard Stiegler helped me develop:
– In a 2016 post, “Has the World Gone Mad? Perhaps…,” I wrote that Stiegler’s main thesis is that capitalism has gone mad and that the absence of regulation and controls can lead to madness. “Disruption” can be beneficial when followed by a period of stabilization.
– That same year, in “Disruption and Madness According to Bernard Stiegler”, I noted that in ancient Greece, the term Pharmakon referred to both remedy, poison, and scapegoat. Medicine becomes harmful if consumed in excess…

I will therefore read Marion Flécher’s book with great interest and will write to you in a future post to see if I find cause for resignation or optimism regarding the startup world.

Post-scriptum: I regularly wonder about the nature of French society’s relationship with science and technology. All the pitfalls of technology are clear, and I regularly mention them here; for example, I’m thinking of François Jarrige’s *Technocritiques*. I’m not sure that the criticism is as severe for science or mathematics, as if they were more neutral. We hear less often about the fact that very few women have been Fields Medalists: two female laureates in 2014 and 2022, compared to 80 laureates in total since 1936.

Science in the media is neglected in France, generalist journalists and even French intellectuals have a rather deplorable scientific culture. Science doesn’t attract many girls, or at least they are discouraged from pursuing it for complex reasons. This wasn’t the case in the former Eastern Bloc countries (whatever the reasons may be). The relationship with technology, and therefore with innovation and startups, is perhaps a consequence of this, or simply a correlation. This might explain some of my sadness or frustration, even though I haven’t lost my enthusiasm. And in those moments, Churchill’s quote comes back to me: “Success is going from failure to failure without losing your enthusiasm.”

Two references in French.

– Mathématiques : deux femmes récompensées depuis 1936 : https://www.lemonde.fr/les-decodeurs/article/2019/03/20/mathematiques-deux-femmes-recompensees-depuis-1936_5438858_4355770.html

– Maryna Viazovska, deuxième femme lauréate après Maryam Mirzakhani : https://information.tv5monde.com/terriennes/medaille-fields-maryna-viazovska-deuxieme-femme-laureate-apres-maryam-mirzakhani-2933

Nexthink, a Lausanne-based startup, acquired for 3 billion dollars

Leave a reply

This doesn’t happen that often in a lifetime [1], so it deserves a pause: Nexthink, a spin-off from EPFL, has just been acquired for $3 billion [2] — you read that right, $3 billion!! Admittedly, Nexthink isn’t exactly young anymore; it was co-founded in September 2004, by Pedro Bados, who came (I believe, to do a master’s internship as part of the Erasmus program) in the artificial intelligence lab. AI wasn’t what it is today. His project was based on Bayesian methods… As luck would have it, I met Pedro then to analyze the intellectual property he had generated and what could be done with it. Pedro wanted to sell the patent that EPFL had filed, and when he discovered it wasn’t generating as much interest as he had imagined, I suggested, “Why not a startup?” That became my main role. I also helped him structure the initial deal, I mean who he would work with, within EPFL and outside, and made some introductions at the time. The rest is history !

Pedro has become a discreet but essential figure in the Swiss ecosystem [3]. He was our guest for ventureideas as early as 2006, along with Jordi Montserrat.

Here are notes taken at the time from his présentation (pdf).
NEXThink notes

He also gave a beautiful interview ten years ago to the newspaper Le Temps (in French): Nobody is ready to be an entrepreneur

I’ve had some wonderful experiences in my professional life, in scientific research first between Paris and Stanford University, then in venture capital with Index Ventures, finally at EPFL for 15 years, and for the last 6 years at Inria. Nexthink will certainly remain one of the best ones, and I hope to experience a few more. As I said 15 years ago [4], my professional passion is to encourage these kinds of ventures (see the Stanford interview): “A love of entrepreneurship, a passion that I took back home to Europe after studying here [at Stanford University]. I want to see a stronger entrepreneurial culture there, and I am working in more than one way to effect that change.”

A few notes:

[1] I was struck some time ago by this post about Index Ventures and its stratospheric performance :

8 startup with an exit above $10B : Figma – $59B, Revolut – $75B, Adyen – $44B, Robinhood – $82B, Scale – $14.9B, Wiz – $32B, Datadog – $46B, Roblox – $86B. So what does $3B represent for Index? And I don’t have a list of their exits above a billion. I remember Virata, Numerical Technologies, The Fantastic Corporation, and Skype before 2005. I might ask them!

[2] Some more news and archives – What I found online about Nexthink acquisition, mostly LinkedIn posts by its founders and investors as well as press articles
Nexthink News autour acquisition

Neil Rimer (Index ventures) and Pedro Bados I am not sure where and when

[3] A short presentation of the EPFL ecosystem to its alumni before 2010 that mentions Nexthink (pdf)

a3angels10-herve_lebert-innogrants

[4] Thanks to my favorite search engine, an exchange about what I thought of startups, Silicon Valley in 2008 where I mention Nexthink. I am not sure things have changed that much…

Stanford HL

Why is Silicon Valley Silicon Valley ? A debate initiated by AnnaLee Saxenian

Leave a reply

I should go back to Silicon Valley to ask AnnaLee Saxenian what she thinks of Silicon Valley today and, more importantly, if her analysis is still valid today (which I think it is !)

I fall by accident on a short 6-page article that she wrote in 1999 entitled Comment on Kenney and von Burg,‘Technology, Entrepreneurship and Path Dependence: Industrial Clustering in Silicon Valley and Route 128’ that you can easily find on the net, for example on Researchgate.

Why do I care about a 25-year old article about innovation ? Because I often have the feeling Europe and France in particular miss the point about what matters. Saxenian’s argument can be summarized with an extract from that article: It is precisely the openness, multiplicity and diversity of interconnections in Silicon Valley that allows economic actors to continually scan the environment for new opportunities and to invest in novel technologies, markets and applications with unprecedented speed. The autarkic structure of firms and institutions in Route 128, by contrast, have historically discouraged precisely the decentralized flows of information, skill and capital that encourage such technological experimentation. [Page 5]

The analysis is subtle because one might get the impression that Europe has understood the role of collaboration, but I fear that it has remained institutional and not informal. Has there ever been a Wagon Wheel Bar in Europe?

Again the article is short and worth reading. The debate is also about the role of big firms in technology clusters. The figure which follows is a perfect illustration:

Source: J. Zhang (2003) compiled data from VentureOne based on VC-backed spin-offs from 1992 to 2001

Zhang had worked with Saxenian and the table shows that from an academic standpoint, entrepreneurship was as strong at MIT/Harvard as Stanford/Berkeley. But if we just look at IBM West vs. IBM East, the difference is striking. “Individuals in Silicon Valley regularly leave jobs at established firms to join start-ups, and vice versa, all the while maintaining networks of cross-cutting personal and professional relationships. Nor is it uncommon for individual engineers working at large firms to make angel investments in promising start-ups — or for established firms to organize venture divisions to support new ventures in related industries.” [Page 4]

I have been using it since I discovered it years ago, particularly when I was giving classes about startup and Silicon Valley. With a little nostalgia, I put my introductory pdf below where I emphasized on the role of culture in entrepreneurship.

eLab01 - SiliconValley

Coreweave, another IPO, more IPOs and the link to VC

Leave a reply

I should thank a colleague of mine for mentioning the surprising not to say crazy IPO of Coreweave. A new cap. table in my list which has now 948 companies. I will update my stats in the final pages of the pdf (available at the end of the post) when I reach 1’000 companies except I have been struggling with IPOs in the recent years. I will expand on this after the Coreweave case.

It’s really a strange story that I did not know and discovered on Wikipedia. 3 founders who were commodity traders launched a crypto currency mining company with obviously a data center and tons of GPUs. They pivoted in 2019 to providing cloud computing in a very aggressive manner. There is a 4th cofounder, the CTO but he apparently joined with the pivot (and mostly own stock options). A crazy growth in revenues (and losses) as the quaterly results show in the next table. Apparently there is cautiousness becuase Microsoft represents 60% of the revenues and the debt is alos about $800M. Impressibe but maybe fragile…

Now the IPOs !

The figure above represents the number of companies in my pdf by year of exit (mostly IPO filings, and much more rarely M&As). [Of course I do not have all IPOs and I found a document which shows I have 27% and 87% of the IPOs of years 2011-22.]

I had forgotten there was such a bubble and crash in 2021 so I had a look at VC investments over decades which gives the following figure. But with so few IPOs, LPs will become more and more impatient putting pressure on VCs all the more money is not as cheap as before…

Now when I hear that VC is in a crisis and I look at the levels of investments in the 7 years compared to the previous decades, I cannot help btu think there is a lot of money available…

Finally the promised pdf, but at this rate it will take me another two years before I release new statistics : Equity in start-ups – Historical data from 900+ companies.

20250717 Equity List Lebret

David Graeber, The Dawn of Everything & Bullshit Jobs

Leave a reply

This post has nothing to do with the startup world. David Graeber was an American anthropologist, author of Bullshit Jobs and co-author of The Dawn of Everything, two books as astonishing as they are stimulating.

The author is “one of the most influential intellectuals in the Anglo-Saxon world.” He can be described as an anarchist, very left-leaning, with a great distrust of centralized institutions and politics. I will simply copy the summary of these two books, which are among the most fascinating I have read in recent years.

A dramatically new understanding of human history, challenging our most fundamental assumptions about social evolution—from the development of agriculture and cities to the origins of the state, democracy, and inequality—and revealing new possibilities for human emancipation.
For generations, our remote ancestors have been cast as primitive and childlike—either free and equal innocents, or thuggish and warlike. Civilization, we are told, could be achieved only by sacrificing those original freedoms or, alternatively, by taming our baser instincts. David Graeber and David Wengrow show how such theories first emerged in the eighteenth century as a conservative reaction to powerful critiques of European society posed by Indigenous observers and intellectuals. Revisiting this encounter has startling implications for how we make sense of human history today, including the origins of farming, property, cities, democracy, slavery, and civilization itself.
Drawing on pathbreaking research in archaeology and anthropology, the authors show how history becomes a far more interesting place once we learn to throw off our conceptual shackles and perceive what’s really there. If humans did not spend 95 percent of their evolutionary past in tiny bands of hunter-gatherers, what were they doing all that time? If agriculture, and cities, did not mean a plunge into hierarchy and domination, then what kinds of social and economic organization did they lead to? The answers are often unexpected, and suggest that the course of human history may be less set in stone, and more full of playful, hopeful possibilities, than we tend to assume.
The Dawn of Everything fundamentally transforms our understanding of the human past and offers a path toward imagining new forms of freedom, new ways of organizing society. This is a monumental book of formidable intellectual range, animated by curiosity, moral vision, and a faith in the power of direct action.
From the publisher website.

Does your job make a meaningful contribution to the world? In the spring of 2013, David Graeber asked this question in a playful, provocative essay titled “On the Phenomenon of Bullshit Jobs.” It went viral. After one million online views in seventeen different languages, people all over the world are still debating the answer.
There are hordes of people—HR consultants, communication coordinators, telemarketing researchers, corporate lawyers—whose jobs are useless, and, tragically, they know it. These people are caught in bullshit jobs.
Graeber explores one of society’s most vexing and deeply felt concerns, indicting among other villains a particular strain of finance capitalism that betrays ideals shared by thinkers ranging from Keynes to Lincoln. “Clever and charismatic” (The New Yorker), Bullshit Jobs gives individuals, corporations, and societies permission to undergo a shift in values, placing creative and caring work at the center of our culture. This book is for everyone who wants to turn their vocation back into an avocation and “a thought-provoking examination of our working lives” (Financial Times).
From the publisher webiste.

Deeptech Startups and their Challenges in France (continued)

Leave a reply

As indicated in my previous article, I preferred to cut out my summary of the workshop on the subject “Deeptech: are we ready to scale?” organized by Inria during the Vivatech trade fair

If the first round table spoke about bipeds, the second was about ecosystems, about “rain forests” more than “French gardens”!

Antonin Bergeaud, I listened to you when you received the award for the best young economist in France, particularly about technological innovation, on France Inter and France Culture and you said at one point that you were drawing a parallel between your childhood dream of being an astronomer and your situation as an economist by saying that you wanted to understand the complexity of the world but that in the economy, there is the human factor which there is not with the stars. Is that our challenge or are there other elements that interest you so that we have European Gafam tomorrow?

“We have the impression that the level of complexity is really in hard sciences but in the human sciences there are a lot of interactions that make things very complicated and in particular because we have little regularity so we have to deal with the fact that there are biases. Like what was mentioned that in Europe we are less enthusiastic than the Americans, but we don’t know how to measure this very well. There are a lot of features that we have to take into account and since the challenge is to try to inform and shed light on why we have such difficulties, for example having a Tech sector that is of the same magnitude as the one we have in the United States or why companies have difficulty obtaining financing in Europe, we are obliged to take into account all these dimensions and it is true that it is quite complicated, so that is a bit where the parallel ends, it is that it is complicated. I think that now there is a kind of consensus beginning on the structural difficulties that we have in France and in Europe, which does not mean that we are going to correct them but at least we are beginning to understand a little better what is happening.” […]
– we don’t have enough entrepreneurs and we don’t have enough engineers trained in France and Europe […] there’s a real training issue that needs to be addressed, largely because you have a lot of losses, a lot of entrepreneurs and engineers leaving for the other side of the Atlantic.
– the second difficulty in Europe, because all the French problems are quite real everywhere in Europe, is getting universities to connect with businesses. For example, all patents filed by all companies in the world must provide the academic references they use in the patent description, and what we see is that for certain technologies, where Europe is practically non-existent in terms of technology production and marketing, we are actually relatively dominant or at the same level as the United States in the production of ideas, except that these ideas are not cited by French or European patents; they are cited by Chinese or American patents. So, basically, we have scientists and researchers who produce very relevant ideas, including on very, very recent technologies, and ideas are supposed to circulate freely. They circulate freely, but they circulate a lot from Europe to other countries, and a little less in the other direction.
– the third problem is indeed financing, which was discussed a lot earlier. I think that in Europe we have a relationship with risk that is really specific to our continent. Perhaps it is not necessarily negative, and I don’t think we should necessarily give it up, but we must be aware that it poses a certain number of difficulties in growing companies quickly, particularly in disruptive technologies, because we tend to move more towards bank financing, because we have less venture capital funding, because we have a market that is very fragmented, particularly in terms of financing innovation, and because we have institutions and regulations that are much more restrictive, at least from a growth point of view, than what is done in the United States.

Paul Midy, I could call you Mr. Start-Up at the National Assembly. What would you like to add?

“I would put the issue of financing number 1 by far. Fundraising in Europe seems to be three times lower than fundraising in the United States, even though we are generally roughly the same size, we generate roughly the same GDP. When you put your money into a company like Mistral, a deeptech company, you don’t get it back the following year, it’s at least 20 years later that you get it back; it’s long-term capital. And this long-term capital exists mainly in retirement capital, and so I would say that the number 1 factor is the fact that we have a pension system in France, and many in Europe too, which is a pay-as-you-go system that is not a capitalization system. We don’t have pension funds or we have very few. We have to realize the enormous gaps that this generates in France. Long-term savings and what can look a bit like capitalization are 200-300 billion euros; if I take the whole European Union, it’s 6,000 billion and essentially it’s the democracies of northern Europe at 70%; if I take the United States it’s 42,000 billion. You can supply a New York Stock Exchange with 25,000 billion and supply a Nasdaq with 25,000 billion and on the other side in France you have Paris the Paris Stock Exchange 3,000 billion Frankfurt 3,000 billion London 3,000 billion so we have a stock of capital which is much less important and so for fundraising the result of all this is that our start-ups last year raised 50 billion in the United States it’s 150 billion. […] I call for us to make a CIP, a common innovation policy at least as ambitious as the CAP, the common agricultural policy. A third of the budget of the European budget is the CAP. Another third is the social cohesion funds. Very important. Innovation is less than 10% of Europe’s budget. It must at least be three times more immediately. […] I am a politician, so we are trying to change the system. Either we say to ourselves, it’s a culture, that’s how Europeans are, and they like risk less, they are a little more grumpy and everything, and so there is nothing to be done. I can’t accept that, so I’m trying to understand why the Americans are in a different situation; it’s not genetic. I think we need to set ourselves the goal of making Europe the richest, most prosperous continent in the world, therefore the most innovative, capable of defending itself, and then everything will flow from that.

Alexis Robert, you work for Kima Ventures, which is Xavier Niel’s fund, whose recent book “Une sacrée envie de foutre le bordel” (A Real Desire to Cause Trouble) I read, and which sometimes puts himself at odds with the system. Do you also, by working for the Kima Ventures fund, have a slightly more atypical view of these things, or how do you want to build on what we just shared?

“In fact, what happens when you are early stage, while what you mentioned is true in late-stage for Series B financing and above, but in fact today what we see is that in the seed rounds, preseed/seed there is in fact a little too much capital, and in fact today the VCs, the problem that there is and why we have difficulty finding GAFAMs is if we actually go back to the history of French venture capital, in fact they are spin-offs of banks and then over time they actually recruited the sons of their LPs [Limited Partners] or people who were in their network or people who thought like them who actually have a finance mindset. There are very few engineers, very few scientists who are actually in these VCs. […] To create GAFAMs, to create for example openAI, Sam Altman comes from the world of Computer Scientists, look at Elon Musk, he is a Computer Scientist, you look at Mark Zuckerberg, he is a Computer Scientist, and in fact to create the GAFAMs of tomorrow it will actually come from people who have a strong scientific culture or who have cultures that are different it can be people who perhaps did not graduate from engineering schools, people who are very different but the VCs are stuck in a mindset and the people in the ecosystem in general too. […] For example Mistral at the time when Arthur Mensch, Guillaume Guillaume Lample and Timothée Lacroix did their first fundraising, uniformly all the VCs all said ah yes what they do is great “yeah but hey they are researchers anyway”, they do not know how to break out of the mold of CEO who went to HEC.”

Mehdi, we supported you at the start-up studio, but before talking about business, we’ll come back to that later. I remember maybe you don’t want to talk about it too much, but you wrote a wonderful essay on what a functioning ecosystem is for entrepreneurship. I reread it two days ago, it was in 2017 I think. Do you have the same vision of the ecosystem’s weaknesses and what a country must do to promote people like you 8 years later?

“So yes, and even more unfortunately, even more so, and I’ll explain why. Yes, money is an issue, but even Sam Altman today, who is at the head of OpenAI, who has just made, who has just said that he has an annual turnover of 10 billion, has financing problems. But for me, the problem, the big problem in the ecosystem, is ambition, it’s the ambition of European entrepreneurs. In California, he would tell you, “I’m going to change the world,” they have an ambition that has no limits, and be careful, it’s not genetic, they are trained for that, they have accelerators like Ycombinator, they have advisors, they are often coached by other entrepreneurs who have had exits or who have made very large companies, and they are fueled by ambition, which I think we lack here. [What’s also missing] is investors who also work on feeling, who work on entrepreneurial ambition, who will go and fight for a billion or a hundred billion dollar case. Money is not the main problem for me because there is money, especially in seed funding in France with the BPI. After that, it is the ambition that must match, and the execution of course, the execution is not simple, but Arthur Mensch raised 100 million on slides in 3 months because he had an ambition at that time. “Unfortunately in Europe we are still in an ecosystem where we make technology with money where others make money with technology.” […] Sam Altman coached close to 1000 startups when he was at the head of Ycombinator, he saw an ecosystem, he saw innovators, he trained himself, that’s why today he says we will make a generative AI, an AI that will be a company that makes 1 billion, a person will be able to make a billion in value thanks to an AI and a only employee but because they are trained. Now look these are what Alain Damasio calls hyperstitions [https://en.wiktionary.org/wiki/hyperstition] we are beyond superstition sometimes, we fall into lies, we fall into ideology so we in Europe we are a little more careful. [In the USA we say] “go for it, go for it, we support you, we will go with you” but today I do not know anyone in Europe who would act like that because they are trained in the USA. It is really an INSEP of entrepreneurs that we need.” […] Entrepreneurship is like playing poker you have cards in hand and then there are cards that arrive and as you go you have to adapt. We need people who will free us up, not just as entrepreneurs!, but who will free up the bandwidth to be able to understand what is happening. For me, these are advisors who have made the Champions League.”

Alexis Robert: “I am very aligned with Mehdi […] there are [so many people who] reject you because in fact you do not speak in the languages of the mold. In fact that is the problem today, is that in fact the entrepreneur feels alone and certain types of entrepreneurs who have a scientific and technical background do not know where to turn and today what is happening in San Francisco, what makes San Francisco great, is because in fact you get off the plane directly you have the feeling of being accepted as a geek, you have the feeling of being at the right place, you have “role models” who are there for you, who pull you up, you have the feeling that you too can be able to do this and in addition there is a sense of community which is extraordinary; you arrive, you are in the street, you speak with a VC, well, he listens to you or not, you have Sam Altman who passes in the street and you can say hello, you sit in a cafe and you talk, you have entrepreneurs to talk to, speaking is easy, introductions are easy and fluid, you can surround yourself with people who allow you to learn and improve because, as was said in the first panel, if you have understood general relativity, succeeding in pitching is not very complicated, you will succeed in doing it and in fact that’s what I wanted to say.”

I stop here and the people said much more. This is unfair not to share everything… But I think it gives you a feeling of what are challenges and opportunities are !

The Tour Triangle designed by Herzog and de Meuron, at the exit of Salon Vivatech, see also Instagram

Deeptech Startups and their Challenges in France

Leave a reply

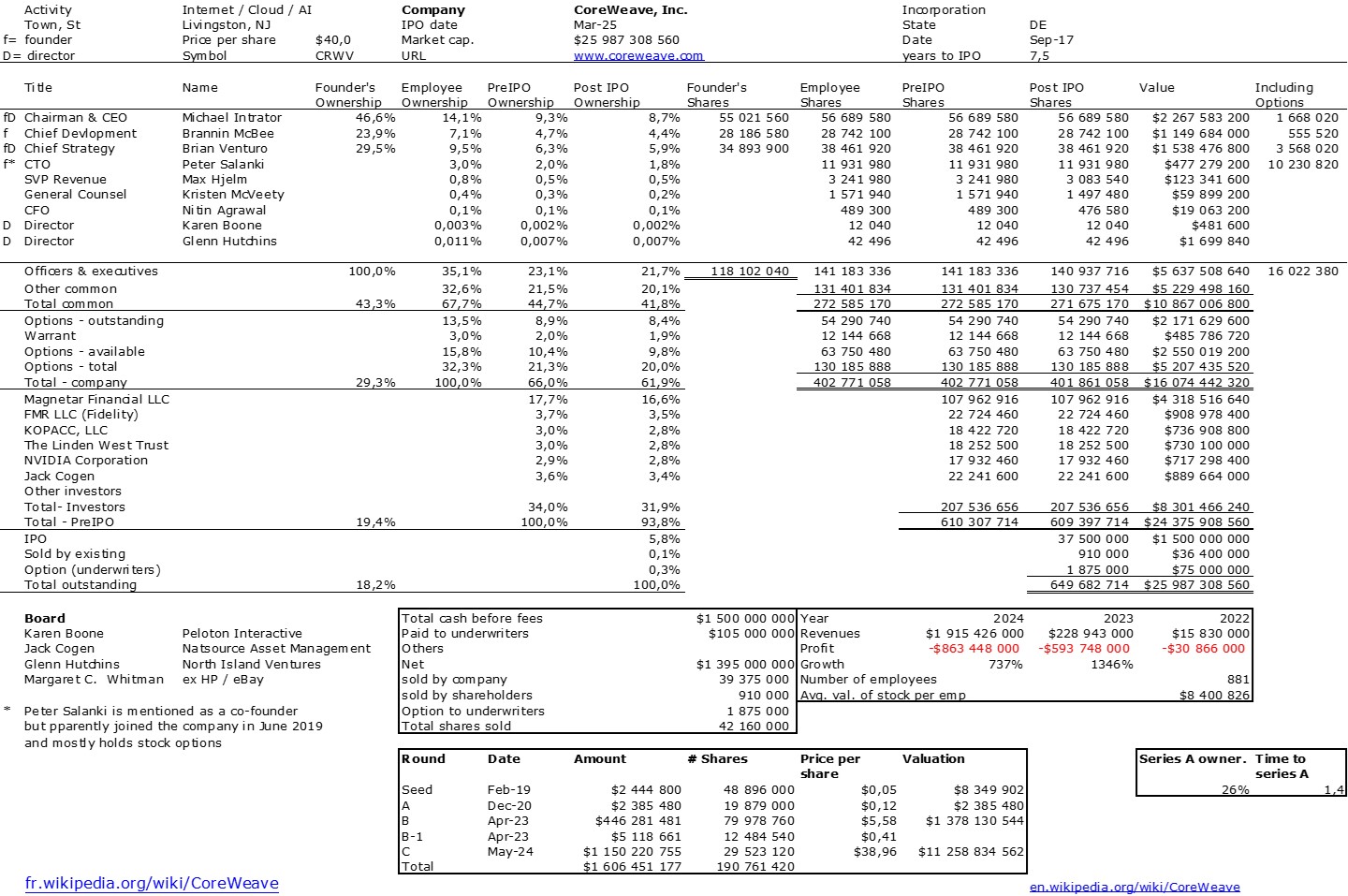
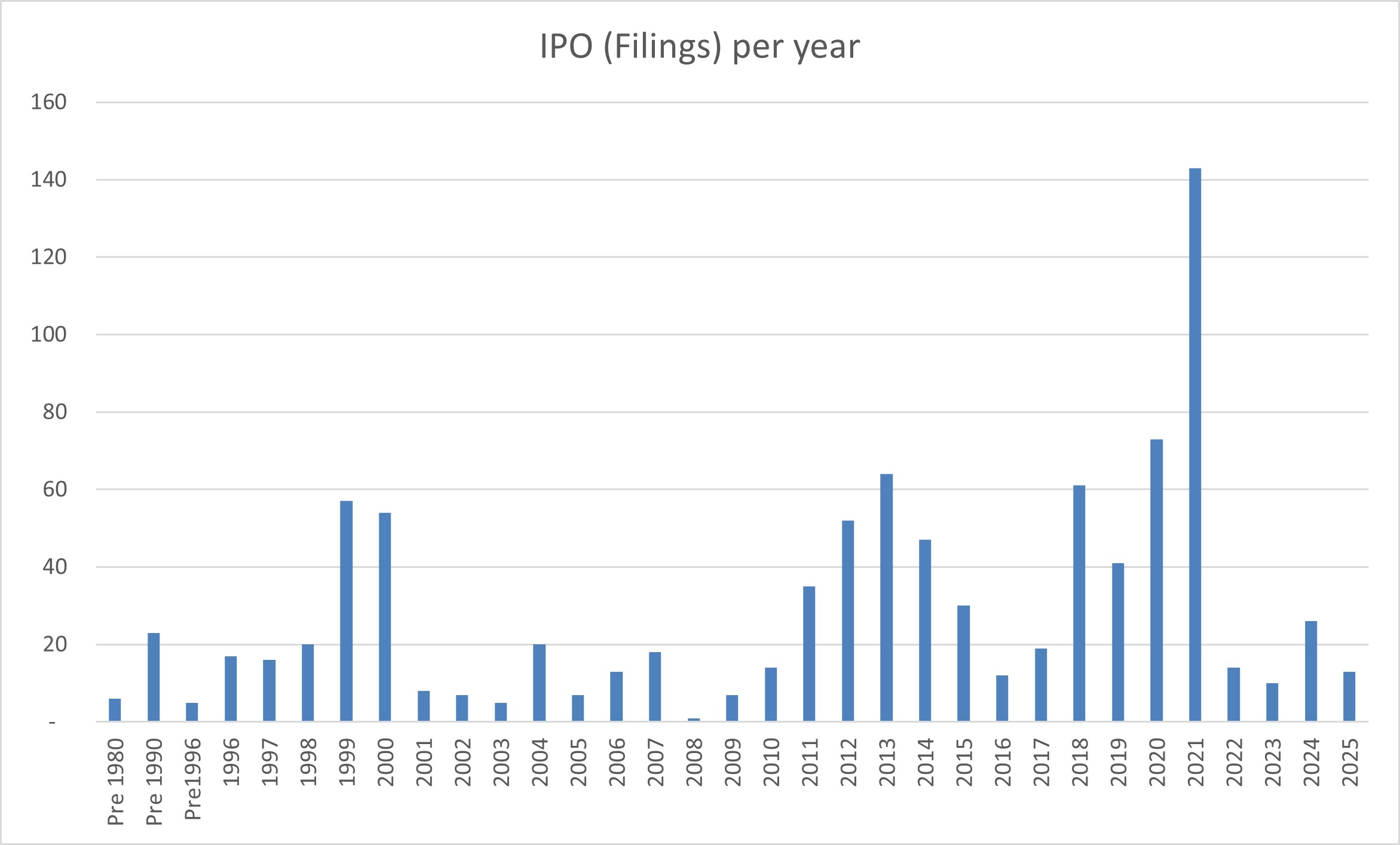
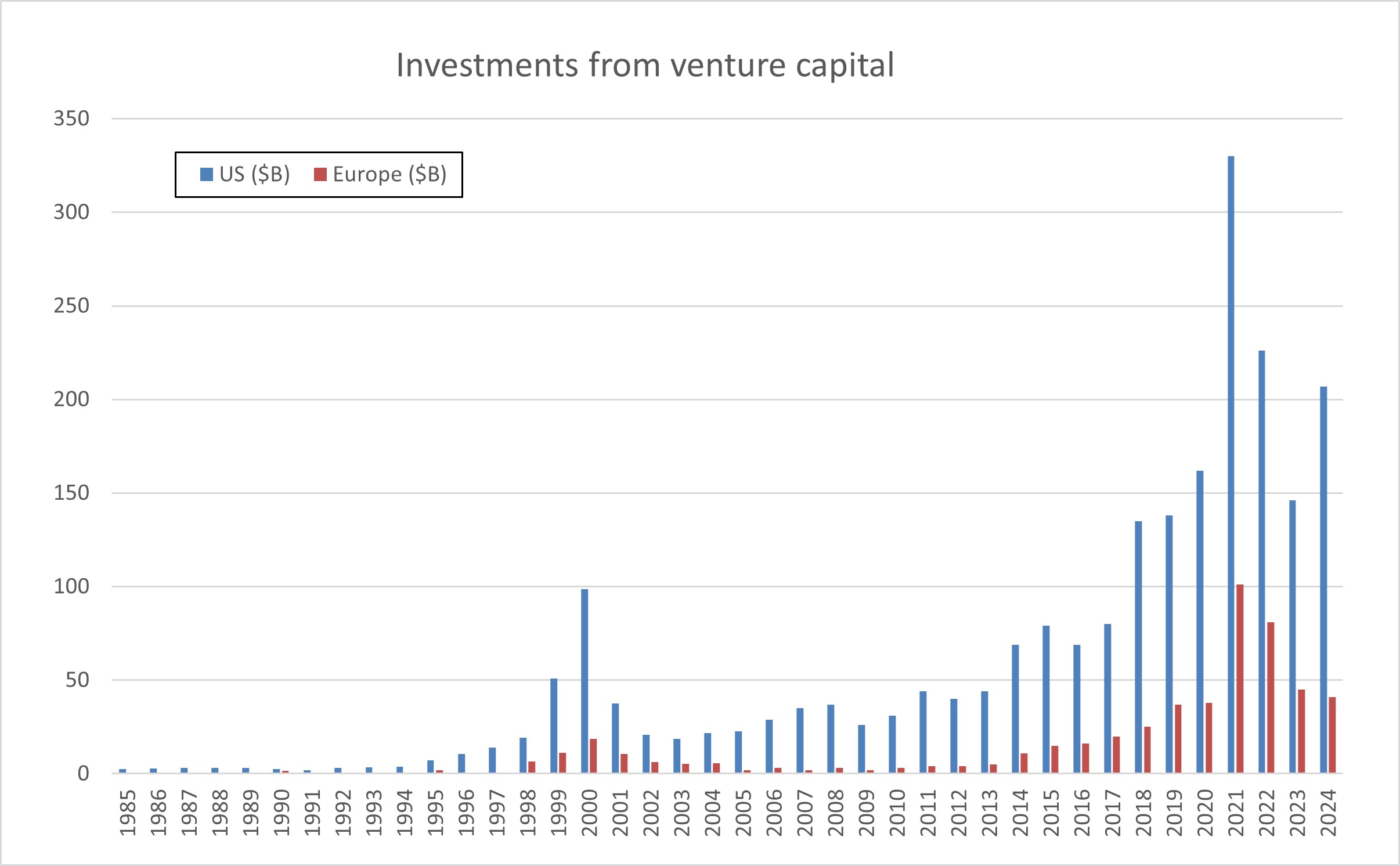
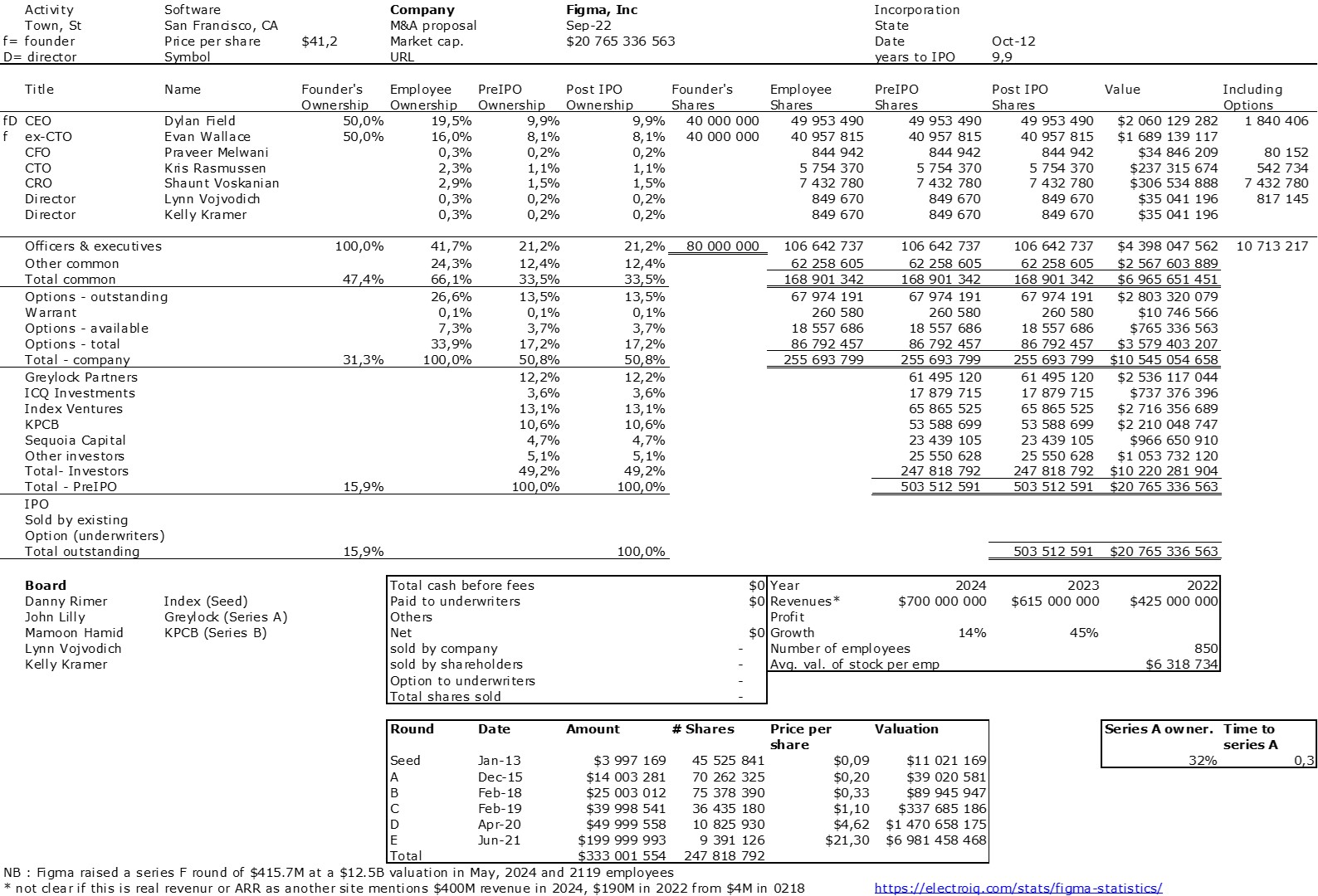
During the Vivatech trade show, Inria organized a workshop on the topic “Deeptech: Are we ready to scale?”

The discussions were rich, in-depth, and fascinating. I’m obviously biased since I was a co-organizer, but I’ve rarely had such a pleasure discussing the topic. So, I’ll provide a subjective summary, adding my own comments on various topics that are dear to my heart. [They will be in brackets and italics.]

What is Deeptech?

This was the starting point for Théau Peronnin, founder and CEO of Alice & Bob. “Above all, it’s a technology that has two fundamental attributes: the first is it has very deep roots in science. If you can understand this technology straight out of business school, it’s perhaps because it’s not quite deeptech yet. […] Its second attribute is the ability to create companies, players, or products that will have a strategic impact on the economy.”

[During another roundtable, I heard that the term appeared when the internet, B2B/B2C, and SaaS had diluted the technology into the excesses of “pet.com”, but that fundamentally, the high-tech of the 1980s and the deeptech of the 2010s are two sides of the same coin. I would add that if something is patentable, it’s undoubtedly deeptech.]

Théau Peronnin then gave his perspective on the challenges facing the French ecosystem. “I can tell you very simply: in France, we are extremely strong on the initial opportunity, we have incredible talent. We are still tied for first place in the number of Fields medals with the Americans, even though we are five times fewer in number.” […] “And then we have an early-stage venture capital ecosystem that has managed to establish itself in recent years, perhaps even a little too much; we could finally say that it is slightly saturated.” […] “The weaknesses are really in the later stages of a deeptech’s life. We have a subject that is perfectly known but which is far from being cracked, which is that of financing the so-called growth stages, this moment when companies like Alice and Bob will seek to raise capital of several tens of millions of euros, several hundreds of millions of euros to continue this R&D race at the international level.” [This is a subject that will be addressed later and I am not sure that it is the main subject, but the debate undoubtedly exists. See below!] “There are no suitable European players, which creates an anticipation effect across the entire value chain and there is a certain reluctance among funds to really deploy this capital with intensity and audacity in deeptech.” […] “Silicon Valley takes its name from the deeptech of the 70s, 80s, 90s in silicon, which created generations of fortunes of individuals with a very strong appetite for this deeptech and who therefore subsequently directed their capital towards these investment funds which continue to invest in this field. In Europe, there are no such fortunes, they were made elsewhere, they are in other fields and therefore we do not yet have these good products, hence the important role of the State in priming the pump.”

“One last point to introduce the round table on the human factor, which is the relationship to risk-taking. France has a school in any case, a view of studies and the academic world very focused on excellence which is perhaps the downside, or rather the cliché, of saying that we have a certain fear of failure and this is seen in my opinion in certain systems which deserve to be rethought, notably that of the Pacte law for the part-time activity of researchers and there it is a very personal opinion that I wish to share with you which is that of saying that there is no entrepreneurship without risk-taking. You have to get your hands dirty, you have to put your career on the line somewhere, you have to have “skin in the game” as the Anglo-Saxons say and perhaps in this system there is therefore in this part-time activity, a comfort in knowing that you are still well protected within your research organization while trying to enjoy the pleasure of entrepreneurship. In my opinion, we have to go all out and that means being able to come back to the academic world after a startup failure and so perhaps the lever to allow more audacity is to make the academic world more attractive for profiles with hybrid careers that have gone through the world of entrepreneurship. That’s to launch this round table on the theme of the human factor, these men and women who are making the entrepreneurs of tomorrow.”

Deeptech is, above all, about bipeds!

Théau Peronnin returned to the subject of humans through a real problem: “A very difficult issue we have is that of parity, gender diversity, which is horribly difficult to crack because we arrive at the very end of the food chain for training these profiles. Above all, technical profiles, a lot of self-centeredness regarding the fact of going through the Grandes Ecoles with all the sociocultural bias there is in these Grandes Ecoles, and even with international diversity, we must have between 20 and 30 nationalities, 30% of non-French speakers in the team, so this gives you a little demography.”

Xavier Duportet amplifies this human aspect: “We have people who are a little crazy because to get started in deeptech [where] less than 2% of projects reach a mature product on the market […] to get started you have to be a little crazy, you have to be naive too, I think, and you have to think that what is impossible can become possible. There are lots of things we don’t know and so the unknown is part of our daily work.” […] “The most important thing for us is not necessarily experience, it’s above all curiosity and that people are enterprising because in deeptech you can’t just apply the principles, apply the things you’ve already learned, you always have to be ready to face failure almost every day and so you need people who are willing to question themselves and who deep down are truly enterprising people.”

Jean-Michel Dalle: “There are motivated bipeds who come to talk to us about the microbiome, or motivated bipeds who come to talk to us about quantum computers. Anyone who doesn’t see things from that perspective, that is, from the bipeds’ perspective, is missing something. Of course, we’re going to check that the quantum computer project isn’t just anything, that they didn’t invent it on a Sunday morning after the market. But if we don’t look at it through the eyes of the founders, in my opinion, we need to change careers.”

Théau Peronnin: “The real issue is that the researcher’s passion is to understand, but the problem with that is that we reap the rewards of the pleasure of our work very early in the product’s life. I understood what I had to break to bring this machine to market, but unfortunately, we only did 5 or 10% of the work to truly deliver the system.” Behind this, we need to strengthen, produce, distribute, reposition. There is a whole issue: how do we learn to take pleasure not in having understood but in making the other person understand, but even more than that, in making the other person adopt what we have cracked, and that is a muscle to develop which is quite different.

Xavier Duportet: “It’s not a technology, it’s not a science that’s going to change the world or save the world, but a product, and that’s often where it falls short. We still see a lot of researchers who only think about science, only technology, and who can’t make the switch in their minds, saying, ‘How come I’m not selling my science, but I’m making people dream, I’m making these serious people [investors] dream, that I’m going to be able to be that person who will transform science into a product that will generate added value for society, but above all, for investors.'”

Marie Paindavoine: “I was lucky at the beginning to be supported in entrepreneurship by structures from the academic world, first by INRIA and then by the University of Berkeley in the United States, which has an acceleration program, and it’s true that thanks to them, it allowed me to learn how to transform this scientific discourse into an entrepreneurial discourse; and moreover, at the acceleration program at the University of Berkeley, for six months, we just repeat the company pitch and learn how to convince, in fact, because ultimately, and they tell us, ultimately, you’ve done the hardest part, you have great technology, you’ve managed to write a thesis in cryptography, well, you’ve done the hardest part, Marie, now learning marketing will take you two months, but you have to get down to it for two months, and that’s where we need to surround ourselves, to have this ecosystem that allows people to train because, after all, if we’ve managed to do a doctorate, we’re able to continue to train in the profession of entrepreneurship, but we need to find those people who can see not the value of scientific technology as it can be presented today, but a sort of projected value of this technology.”

Xavier Duportet: “On people and the network and the ecosystem, I also had the chance to do a thesis between INRIA and MIT. At first I wanted to be a researcher and when I arrived at MIT, I saw all these people who were starting up, these professors who were becoming entrepreneurs, that’s when I understood I was inspired by this generation of entrepreneurial researchers saying to myself but in fact if we really want to change the world it’s not research it’s entrepreneurship and today in the US, there is Silicon Valley, it was created 20 years ago, 30 years ago as Théau said there is this whole generation now, not grandpas but slightly older people who have succeeded and so in fact there is a “network effect” in the US which is super important, it’s the generation of entrepreneurs who have already succeeded who are there to help and pass on they did it they made mistakes and they really serve as mentors and that’s where we have a pretty interesting opportunity, and in France we can’t want to put the cart before the horse, we have what the BPI has done, all the research institutes, the change that has been underway for 10 years, we are starting to have these companies which are becoming leaders on the international level.”

Matthias Schmitz: “What we have started to do recently is to invest in an entrepreneurial mindset much earlier in the education of our students so we are trying to roll out programs where we bring entrepreneurship into all the faculties. For example, the university of Saarland is investing €1.5M every year with the goal that every single student that we have, whether it is a business student, whether it is a Romanistic student or an engineering student has at least one time during his studies thought whether entrepreneurship can be a career option for himself and by doing that I think we try to solve the problem a little bit earlier, bring the mindset in the heads of the people and not having to have people jump into the too cold water at the moment where they are already at the PhD level.”

Marie Paindavoine on being a female entrepreneur: “do you want the version we hear in France or the United States? both! So we don’t hear the same thing in France and in the United States. In France, I was immediately asked if I intended to partner with “un” CEO, emphasizing the “un”. I was already asked after my presentation, well, anyway, I’m not going to do them all actually because it’s of no interest, but there is indeed a halo of suspicion, let’s put it like that. In the United States, then I’m not saying that they are better than in France because I arrived at the University of Berkeley, at the University of Berkeley accelerator, 2,000 applications, 30 start-ups selected, 2 women CEOs, so they are not much better. On the other hand, once we reach this level of selection, when I say I’m starting a business with children, people tend to congratulate me on the level of energy it requires instead of asking me how I’m going to arrange childcare and if my husband agrees with me starting a business with my children, something I’ve already been asked in France.

I’ll stop here and do a new post about the second roundtable!

Figma again, now an IPO

Leave a reply

I published a post about Figma in October 2022 when it was announced it would be acquired by Adobe for $20B. Here is the article. At the time I could not find official data about the startup and I built a cap. table based on public data available online (see at the bottow).

This morning I found a SEC filing document published in Nov. 2022 that I had not seen before, which says much more. So I built a revised cap. table and you can compare it also below close to the older one. They are not that different though. My motivation for looking for such a document is that Figma has confidentially filed for an IPO. So if it happens, updated numbers will emerge like fundrasising between 2022 and 2025, real revenues, profit (or loss) and employee count. Still I had to publish this revised version.

Figma cap. table as revised in July 2025

Figma cap. table estimated in October 2022

And cherry on the cake, a LinkedIn post by Danny Rimer :

Google vs. Y Combinator

Leave a reply

“Don’t be evil” Google (former) motto

“Make something people want” Y Combinator (current) motto

What a shock to discover the briefing of Y Combinator “against” Google in the U.S.’s monopoly case against the search giant. The link is here and the pdf there:

govuscourtsdcd22320513001

I have been a fan of both entities for 20 years. But time flies and the world apparently changes. At the end of this post I will come back to the reasons why I have been impressed by Y Combinator over time and in particular the duo Jessica Livingston / Paul Graham.

In fact this article is more about Y Combinator. It could be that what I liked about Google is dead as it was hinted in Goomics. So no real need to talk about Google. I have done it so often with the tag #google. But I first need to describe shortly the accelerator’s arguments against Google.

BRIEF OF Y COMBINATOR, LLC AS AMICUS CURIAE IN SUPPORT OF PLAINTIFFS

The remedies stage of this case has important implications for technology startup founding and funding. We respectfully submit this brief to share our view, based on two decades of frontline experience, that robust antitrust enforcement here can help to foster a healthier, more resilient, and more vibrant U.S. innovation ecosystem. The startups we work with every day should be able to exercise their “vigor, imagination, devotion, and ingenuity,” United States v. Topco Assocs., Inc., 405 U.S. 596, 610 (1972), in markets that are free from restrictive conduct and illegally maintained monopoly power. YC supports Plaintiffs’ proposed remedy package as a whole. To aid the Court’s analysis, we also highlight below particular components of the proposed remedy as to which we believe our first-hand experience has given us unique insight and perspective.

Anticompetitive measure have been constant in the history of the USA and the brief reminds it :

Experience has taught us that technological inflection points are critical moments for competition and innovation. The rise of novel, transformative technology can create an opening for nimble startups to disrupt established incumbents. […] Dominant incumbents often respond by using exclusionary conduct to try to slow down or coopt the future. […] For example, during the mid-1990s, Microsoft recognized the disruptive potential of web-based software applications and reacted by anticompetitively blocking rival internet browsers from reaching users. United States v. Microsoft Corp., 253 F.3d 34, 60 (D.C. Cir. 2001). More recently, Facebook recognized the explosion in usage of mobile applications and reacted by acquiring mobile-native startups that it viewed as competitive threats. See FTC v. Meta Platforms, Inc., No. CV 20-3590 (JEB), 2024 WL 4772423, at *29–30 (D.D.C. Nov. 13, 2024) (“[T]he case for buying Instagram focused heavily on neutralizing a competitive threat.”).

Antitrust remedies have a long track record of unlocking American dynamism and ingenuity. An antitrust consent decree in 1956, for example, required AT&T to provide open access to its patents and technical manufacturing information. That remedy order helped usher in the modern digital age, in large part because it enabled “young and small” firms—what we think of today as “little tech” companies—to compete. See Martin Watzinger et al., How Antitrust Enforcement Can Spur Innovation: Bell Labs and the 1956 Consent Decree, 12 AM. ECON. J. ECON. POL’Y 328, 330 (2020). A new generation was able to enter and expand in a multitude of markets, helping to vault the United States into position as the world’s leader in technological innovation. Id. Economists have called the 1956 antitrust decree “one of the most unheralded contributions to economic development” in history, and the co-founder of Intel called it “one of the most important developments for the commercial semiconductor industry.” This tradition has continued in the modern era. In 2022, for example, the U.S. Federal Trade Commission blocked Nvidia Corp.’s proposed acquisition of Arm Ltd., a semiconductor technology firm. Arm’s CEO later explained that the structural separation “helped us” focus on delivering better products at a time when “more applications [were] moving towards the cloud” and “AI [was] starting to raise its head.” An Interview with Arm CEO Rene Haas. Arm has since gone public on the Nasdaq stock exchange, delivered record revenues, and is now worth more than $100 billion. Meanwhile, Nvidia’s earnings have nearly quintupled as its chips helped to fuel the rise of generative AI technology.

But by foreclosing competition, Google has chilled independent firms like YC from funding and accelerating innovative startups that could otherwise have challenged Google’s dominance. The result is a landscape that has been artificially stunted and stagnant. In our view, Plaintiffs’ proposed remedy package would help to unlock a more dynamic, globally competitive U.S. technology startup ecosystem.

Y combinator proposes the following remedies:
A. The Remedy Should Open Access to Google’s Datasets and Search Index.
B. The Remedy Should Prevent Google from Extending Its Monopolies into Query-Based AI Tools.
C. The Remedy Should Prevent Google From Entering Pay-to-Play Arrangements with Distributors.
D. The Remedy Order Should Deter Circumvention and Retaliation.

I’m not sure I understand all of this, but the implications would certainly be major. I will not go into more details, but for sure this is deep and quite fascinating.

ABOUT Y COMBINATOR

The brief mentions an article about Y Combinator, subtitled The Inside Story of Tech’s Most Influential Startup Accelerator. It is a great reading. I loved it and illustrates with a few comments.

First their philosophy is what mainly attracts me. And once again, this is linked to the people who founded it, in particular Paul Graham and Jessica Livingston. I will not count how many times Graham is quoted here, his essays are famous (I just counted 228 different articles since 2005) and in a way they are close to Montaigne’s. Just check one for example, The Two Kinds of Moderate.

As the article says, Jessica Livingston has an underrated role, “If Paul Graham was Y Combinator’s philosophical architect, Jessica Livingston was its social architect—quietly and effectively shaping YC’s culture and community from the earliest days.” If you have never heard of her, it is never to late to read Founders at Work. And indded Paul Graham felt the need to right an essay entitled Jessica Livingston 🙁

Their philosophy is simple and complex at the same time. Again read the article mentioned above and here are their “mantras, distilled from hard-earned experiences, are now part of global startup culture:

THE PERFORMANCE OF Y COMBINATOR

Don’t get me wrong. All this does not mean Y Combinator has found the recipe for success. Let met add just figures from the article:

You can have you own thoughts about these numbers. What I read is :
– out of 5000 startups, 17 went public (less than 1%) and about 500 were acquired (about 10%) and remember an acquisition can be at a very low value.
– not that many fail, particularly in the first years , so the “fail fast” mantra is not that obvious.
Is Y Combinator more sucessful than others. I do not know but I loved their approach to entrepreneurship.

ABOUT THE EVOLUTION AND DEATH OF INNOVATIVE ENTITIES

I just said “loved” and not “love”. I begin to feel that old structures lose their agility and creativity. It is what Y Combinator thinks of Google. I discovered that Graham and Livingston have retired from YC. I also believe that a culture is difficult to maintain when the founders leave. And I had a similar feeling with YC when Sam Altman & others began to lead it. There is somethind depressing about the comment but maybe not.

My first article on this blog was about the speech of Steve Jobs at Stanford. Read it again and again :

Death is very likely the single best invention of Life. It is Life’s change agent. It clears out the old to make way for the new. Right now the new is you, but someday not too long from now, you will gradually become the old and be cleared away. Sorry to be so dramatic, but it is quite true.

Your time is limited, so don’t waste it living someone else’s life. Don’t be trapped by dogma – which is living with the results of other people’s thinking. Don’t let the noise of others’ opinions drown out your own inner voice. And most important, have the courage to follow your heart and intuition. They somehow already know what you truly want to become. Everything else is secondary.