Comme Guillermo Martinez l’a écrit à juste titre dans un de ses essais, « il est bien connu qu’il n’y a qu’une seule façon plus efficace pour tuer la conversation dans une salle d’attente que d’ouvrir un livre, c’est d’ouvrir un livre de mathématiques ». J’espère pourtant que vous lirez ce qui suit !
Même dans la haute technologie, l’innovation et l’entrepreneuriat, le thème de l’imagination face à la raison, thème qui pourrait être traduit par « la technologie et le marché », est une question récurrente. Alors, quand je lis des livres sur la créativité, que ce soit scientifique ou artistique, je suis toujours à la recherche de liens avec l’innovation. J’ai eu l’occasion de le vérifier à nouveau avec Guillermo Martinez et son Borges et les mathématiques. Borges est probablement l’un des « poètes » qui met le plus de mathématiques dans son œuvre littéraire. Guillermo Martinez qui est à la fois un romancier et un mathématicien a récemment publié en anglais ce joli petit livre sur les mathématiques dans les nouvelles de Borges. J’ai déjà parlé de mathématiques dans un post récent alors laissez-moi ajouter ici quelques mots sur ce que j’ai aimé.

Martinez cite Borges qui cite Poe: « Je crois – peut-être naïvement – aux explications de Poe. Je pense que le processus mental qu’il décrit correspond réellement au processus créatif. Je suis sûr que c’est la façon dont fonctionne l’intelligence: à travers des revirements de l’esprit, en franchissant des obstacles et en produisant des éliminations. La complexité de l’opération qu’il décrit ne me dérange pas, je soupçonne que la véritable approche doit être encore plus complexe et beaucoup plus chaotique et hésitante. Tout cela ne signifie pas pour suggérer que les arcanes de la création poétique ont été révélées par Poe. Dans les liens que l’écrivain explore, la conclusion qu’il tire de chaque hypothèse est logique, bien sûr, mais pas la seule nécessaire ». Borges dans La genèse du Corbeau de Poe.
Et il ajoute plus encore sur le processus créatif: Quant au débat sur l’intuition « divine, ailée » en opposition à la logique, au pas de tortue, prosaïque, je voudrais aller à l’encontre d’un mythe à propos des mathématiques: le processus que Borges décrit est exactement le même que celui qui se passe dans la création mathématique. Prenons le mathématicien qui doit prouver un théorème pour la première fois. Notre mathématicien cherche à prouver un résultat sans même savoir si une telle preuve existe vraiment. Il tâtonne son chemin à travers un monde inconnu, à prouver et à faire des erreurs, à affiner son hypothèse, à tout recommencer et essayer une autre approche. Lui aussi a des possibilités infinies à sa portée, à chaque pas qu’il fait. Et si chaque tentative est logique, en aucun cas elle ne sera la seule possible. C’est comme les coups d’un joueur d’échecs. Chacun des mouvements du joueur d’échecs est conforme à la logique du jeu, afin de piéger son rival, mais aucun n’est prédéterminé. Il s’agit d’une étape cruciale dans l’élaboration artistique et mathématique, et dans n’importe quelle tâche d’imagination. Je ne crois pas qu’il existe quelque chose d’unique à la création littéraire en ce qui concerne la dualité de l’imagination / intuition par rapport logique / raison.
Je crois fermement que l’innovation est très similaire au processus de création artistique ou scientifique. Mais dans un autre essai, Martinez dit plus sur la création: « C’est le même sentiment d’euphorie que vous ressentez lorsque, après de nombreuses années de lutte avec votre propre ignorance, vous comprenez soudainement comment regarder quelque chose. Tout devient plus beau, et vous avez le sentiment que vous pouvez voir plus loin qu’avant. C’est un moment glorieux, mais vous devez payer le prix pour ce qui est votre obsession du problème, comme une plaie constante ou un caillou dans votre chaussure. Je ne recommanderais pas ce genre de vie à tout le monde. Einstein avait un ami proche, Michele Besso, avec qui il a discuté de nombreux détails de la théorie de la relativité. Mais Besso-même n’a jamais accompli quelque chose d’important dans la science. Sa femme demanda un jour pourquoi à Einstein, puisque, en fait, son mari était si doué. « Parce qu’il est une bonne personne! » répondit Einstein. Et je pense que c’est vrai. Vous devez être un fanatique, qui ruine sa vie et les vies des personnes qui lui sont proches. » Encore une fois vous pourriez méditer sur le taux élevé de divorce dans la Silicon Valley et la créativité qui nécessite du fanatisme.
Pour ceux qui s’intéressent vraiment en mathématiques, je ne peux pas éviter de mentionner quelques autres sujets abordés par Martinez: le théorème d’incomplétude de Gödel est l’une des plus grandes réalisations en mathématiques, même s’il est compliqué à comprendre. D’une une manière très simpliste, on peut dire que même en mathématiques, il ya des choses qui sont vraies, mais qui ne peuvent pas être prouvées. Le paradoxe de Russell est presque aussi fascinant mais plus simple à saisir:
Il y a quelques versions de ce paradoxe qui se rapprochent de situations réelles et donc peut-être plus faciles à comprendre pour les non-logiciens. « Un barbier se propose de raser tous les hommes qui ne se rasent pas eux-mêmes, et seulement ceux-là. Le barbier doit-il se raser lui même ? L’étude des deux possibilités conduit de nouveau à une contradiction. On résout le problème en affirmant qu’un tel barbier ne peut exister (ou, en jouant sur les mots, qu’il n’est pas un homme), ce qui ne surprendra personne : il n’y a pas vraiment de paradoxe. Plus exactement la démonstration qui précède constitue justement une démonstration de la non-existence d’un tel barbier. » (Article de Wikipédia)
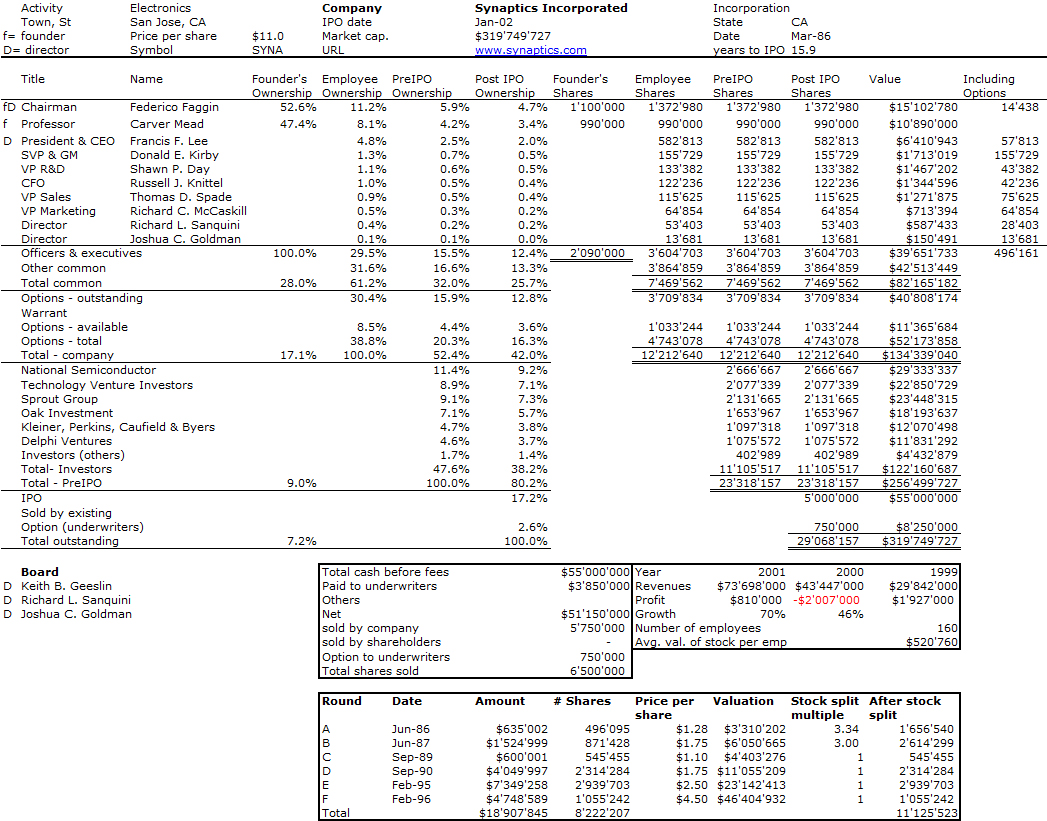
On peut formuler le paradoxe ainsi : « l’ensemble des ensembles n’appartenant pas à eux-mêmes appartient-il à lui-même ? Si on répond oui, alors, comme par définition les membres de cet ensemble n’appartiennent pas à eux-mêmes, il n’appartient pas à lui-même : contradiction. Mais si on répond non, alors il a la propriété requise pour appartenir à lui-même : contradiction de nouveau. On a donc une contradiction dans les deux cas, ce qui rend l’existence d’un tel ensemble paradoxale. » (Article de Wikipédia)
Symboliquement: si
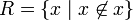
alors