« Les mathématiciens sont les humains qui font progresser la compréhension humaine des mathématiques. »
William P. Thurston

J’avais déjà mentionné le livre de David Bessis, Mathematica, lors du passage sur France Culture de l’auteur. Il y parlait de Grothendieck, mais disait surtout qu’entre logique et intuition, il donnait plus d’importance à la seconde pour faire des mathématiques. Retournez sur l’article pour trouver le lien de l’entretien. J’ai eu la chance de lire son très bel ouvrage ces derniers jours et l’auteur est convaincant. Il y explique assez bien l’échec de l’enseignement des mathématiques qui donnent trop d’importance à la première.

Sans doute sera-t-il difficile de faire changer d’avis les sceptiques, mais l’argument selon lequel il n’y a pas de talent ou de don particulier pour faire des mathématiques mais surtout de la curiosité et de la persévérance, comme pour toute activité qui demande un apprentissage, est bien illustrée dans son livre.

Il n’est pas question d’astuces que l’on emploie trop souvent dans l’enseignement de la mathématique, ce qui peut faire moins aimer la discipline. Dans l’article sur la Beauté des mathématiques, j’employais à tort et un peu trop cette impression de magie. Il est ici question de compréhension profonde des choses, au sens que l’on finit par les voir. L’inconvénient des mathématiques, est qu’alors que la musique s’entend, ou qu’un sport est physiquement visible, les mathématiques sont surtout faites d’images mentales.

Il parle lui aussi (comme j’ai du le faire si vous suivez le hastag #mathematique) des démonstrations de la somme des premiers entiers naturels et Bessis est lumineux quand il explique que la démonstration astucieuse de Gauss ne permet sans doute pas d’en « comprendre » la solution:

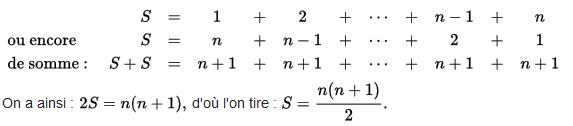
alors qu’il y a des approches plus intuitives comme l’utilisation de triangles ou de distance à la moyenne. Lisez ses pages 169 à 181, on y comprend aisément pourquoi Thurston enfant donna d’abord 5000 comme réponse à la somme des 100 premiers entiers, puis se corrigea pour donner la réponse exacte. La moyenne d’un tirage aléatoire de nombres entre 1 et 100 n’est pas non plus tout à fait 50… (contrairement celle entre 0 et 100) et il y a un lien entre les deux sujets.

J’ai beaucoup aimé les descriptions et portraits que Bessis fait de Descartes, Thurston, Grothendieck et le moins célèbre Ben Underwood. Ou les magnifiques passages sur Pierre Deligne et Jean-Pierre Serre. Je vous laisse les découvrir.

C’est un beau livre à offrir à qui souhaite découvrir ou redécouvrir la beauté des mathématiques. Et peut-être plus important encore, comme l’indique le sous-titre du livre, une aventure au cœur de nous-mêmes, Bessis montre bien que toute exploration est avant tout le choix de dépasser ses peurs, d’accepter la possibilité des erreurs, et la possibilité d’un chemin vers plus de confiance en soi. Un paradoxe est un conseil qui revient souvent dans son livre : « Il ne faut jamais lire les livres de math. » Sauf celui-ci ! Superbe !